이진탐색트리(binary search tree)는 정렬된 값들이 리스트에 존재할 때 주어진 값을 로그 시간 안에 찾는 방법인 이진탐색(binary tree)을 트리에 접목한 자료구조이다. 단순연결리스트에 비해, 저장된 값을 탐색하거나 임의의 값을 삽입하고 삭제하는 연산을 수행하는 데에 시간이 적게 걸린다는 장점이 있다. 이진탐색트리를 직접 구현해본 다음, 이진탐색트리에 기반한 자료구조인 AVL 트리, 2-3 트리, 좌편향 레드블랙트리(left-leaning red-black tree), B-트리에 대해서도 간단히 정리했다.
- 이진탐색(binary search)
- 이진탐색트리(binary search tree)
- AVL 트리
- 2-3 트리
- 좌편향 레드블랙트리(left-leaning red-black tree)
- B-트리
이진탐색(binary search)
리스트 a가 정렬되어 있었다면 탐색에 걸리는 시간은 \(O(log N)\)이다. 만일 정렬되어 있지 않았다면, 순차탐색(sequential search)을 수행해야 하기 때문에 \(O(N)\)의 시간이 걸린다.
# 정수들이 정렬된 리스트 a에서 t라는 값이 존재하는 index를 탐색하기
def binary_search(a, left, right, t):
if left > right:
return None
mid = (left + right)//2
if a[mid] == t:
return mid
if a[mid] > t:
binary_search(a, left, mid - 1, t)
else:
binary_search(a, mid + 1, right, t)
이진탐색트리(binary search tree)
이진탐색트리(binary search tree)는 각 노드 node의 키값이 node의 왼쪽 서브트리에 있는 노드들의 키값들보다 크고, n의 오른쪽 서브트리에 있는 노드의 키값들보다 작은 이진트리이다. 그래서 이진탐색트리에서 중위순회를 수행하면 정렬된 출력을 얻게 된다.
class Node:
def __init__(self, key, value, left=None, right=None):
self.key = key
self.value = value
self.left = left
self.right = right
class BST:
class EmptyError(Exception):
pass
def __init__(self):
self.root = None
임의의 키값을 가지는 노드 탐색하기
# key를 키값으로 가지는 노드의 항목 반환하기
def get(self, key):
return self.get_item(self.root, key)
def get_item(self, node, key):
if node == None:
return None
if node.key > key: # 방문한 노드의 키값이 key보다 크다면
return self.get_item(node.left, key) # 왼쪽 서브트리 탐색하기
elif node.key < key: # 방문한 노드의 키값이 key보다 작다면
return self.get_item(node.right, key) # 오른쪽 서브트리 탐색하기
else: # 방문한 노드의 키값이 key와 같다면
return node.value # 노드의 항목 반환하기
키값이 가장 작은 노드 탐색하기
# 가장 작은 키값을 가진 노드 반환하기
def min(self):
if self.root == None:
return None
return self.minimum(self.root)
def minimum(self, node):
if node.left == None: # 방문한 노드의 왼쪽 자식이 없다면 그 노드의 키값이 가장 작은 것이므로
return node # 노드 반환하기
return self.minimum(node.left) # 왼쪽 자식에서부터 다시 탐색 시작하기
임의의 키값을 가지는 노드 삽입하기
# key와 value를 키값과 항목으로 가지는 노드 삽입하기
def put(self, key, value):
self.root = self.put_item(self.root, key, value)
def put_item(self, node, key, value):
if node == None:
return Node(key, value) # 새 노드 생성하기
if node.key > key:
node.left = self.put_item(node.left, key, value)
elif node.key < key:
node.right = self.put_item(node.right, key, value)
else: # key가 이미 트리 내부에 존재하면
node.value = value # value를 갱신하기
return node
키값이 가장 작은 노드 삭제하기
# 키값이 가장 작은 노드 삭제하기
def delete_min(self):
if self.root == None:
raise EmptyError('Underflow')
self.root = self.del_min(self.root)
def del_min(self, node):
if node.left == None:
return node.right
node.left = self.del_min(node.left)
return node
# 50
# / \
# 30 80
# / \ \
# 10 40 90
# \
# 15
del_min(root):
root.left = del_min(root.left)
del_min(root.left):
root.left.left = del_min(root.left.left)
del_min(root.left.left):
return root.left.left.right # 15
return root.left # 30
# / \
# 15 40
return root # 50
# / \
# 30 80
# / \ \
# 15 40 90
임의의 키값을 가지는 노드 삭제하기
삭제할 노드 node의 자식 수에 따라 처리 방법이 달라진다. 자식이 없는 경우 node의 부모에 node 대신 None을 연결하고, 자식이 하나라면 node의 부모에 node의 자식을 직접 연결한다. 자식이 둘일 때가 좀 까다롭다. 먼저 중위후속자(inorder successor)의 개념을 알아야 한다. 노드 node의 중위후속자는 트리를 중위순회할 때 node 직후에 방문되는 노드이다. node의 자식이 둘이라면, node의 중위후속자를 떼어내서 node가 있던 자리에 올리면 된다. 이때, node의 중위후속자는 node의 오른쪽 서브트리에서 키값이 가장 작은 노드이기 때문에 node의 오른쪽 서브트리에서 del_min() 연산을 수행해주어야 한다.
# 키값이 key인 노드 삭제하기
def delete(self, key):
self.root = self.del_node(self.root, key)
def del_node(self, node, key):
if node == None:
return None
if node.key > key:
node.left = self.del_node(node.left, key)
elif node.key < key:
node.right = self.del_node(node.right, key)
else: # 키값이 key인 노드를 방문함
if node.right == None: # 노드의 오른쪽 자식이 없는 경우
return node.left # 노드의 왼쪽 자식을 반환하기
if node.left == None: # 노드의 오른쪽 자식은 있지만 왼쪽 자식이 없는 경우
return node.right # 노드의 오른쪽 자식을 반환하기
target = node
node = self.minimum(target.right) # target의 중위후속자는 minimum(target.right)임
node.right = self.del_min(target.right) # target의 중위후속자를 삭제한 target의 오른쪽 서브트리를 node에 연결하기
node.left = target.left # target의 왼쪽 서브트리를 node에 연결하기
return node
# 60
# / \
# 50 70
# /
# 20
# / \
# 10 45
# /
# 35
# / \
# 25 40
# \
# 30
del_node(root, 20):
root.left = del_node(root.left, 20)
del_node(root.left, 20):
root.left.left = del_node(root.left.left, 20)
del_node(root.left.left, 20):
target = root.left.left # 20
root.left.left = minimum(target.right) # 25
root.left.left.right = del_min(target.right) # 45
# /
# 35
# / \
# 30 40
return root.left.left # 25
# / \
# 10 40
# /
# 35
# / \
# 30 40
return root.left # 50
# /
# 25
# / \
# 10 45
# /
# 35
# / \
# 30 40
return root # 60
# / \
# 50 70
# /
# 25
# / \
# 10 45
# /
# 35
# / \
# 25 40
# \
# 30
연산의 수행시간 계산하기
탐색, 삽입, 삭제 연산의 수행시간은 이진탐색트리의 높이에 비례한다. 따라서 최악의 경우에 수행시간은 \(O(N)\)이다. 하지만 빈 이진탐색트리에 랜덤하게 선택된 \(N\)개의 키를 삽입할 때 트리의 높이는 약 \(1.39logN\)임이 알려져 있기에 평균 수행시간은 \(O(N)\)보다 작다.
AVL 트리
AVL 트리는 각각의 노드에 대해 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차이가 1 이하인 이진탐색트리이다. \(N\)개의 노드를 가진 AVL 트리의 높이는 \(O(log N)\)이 되므로 탐색, 삽입, 삭제 연산에 걸리는 시간이 항상 \(O(log N)\)으로 유지된다는 장점이 있다.
class Node:
def __init__(self, key, value, height, left=None, right=None):
self.key = key
self.value = value
self.height = height
self.left = left
self.right = right
class AVL:
class EmptyError(Exception):
pass
def __init__(self):
self.root = None
def height(self, node):
if node == None:
return 0
return node.height
회전을 통해 높이의 균형 유지하기
AVL 트리에서는 높이의 불균형이 발생했을 경우 이를 없애기 위한 회전 연산을 제공한다.
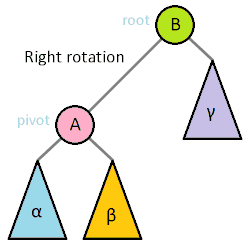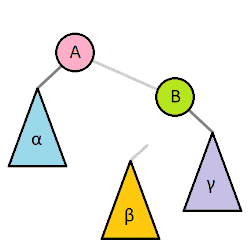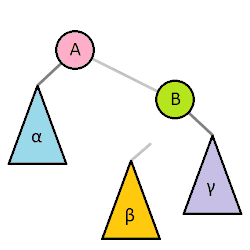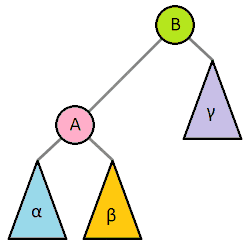
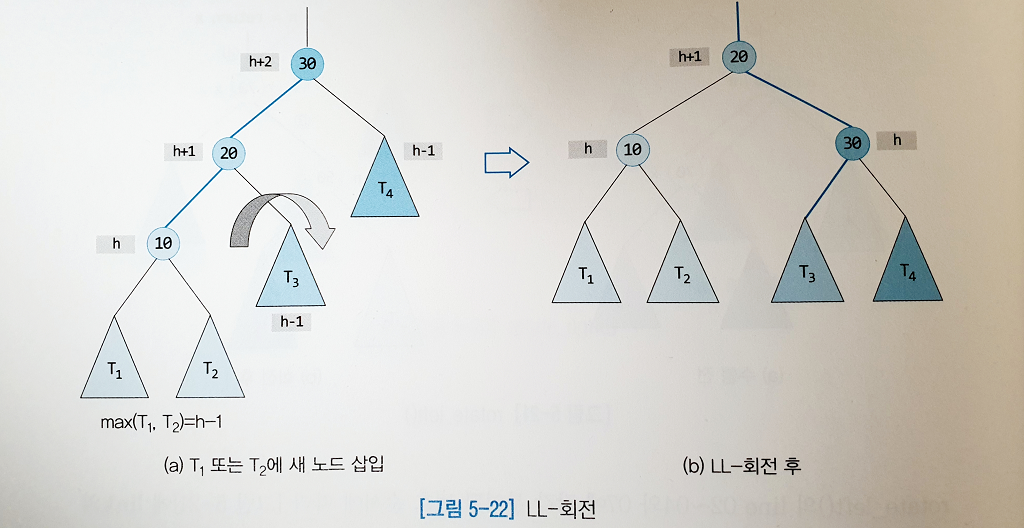
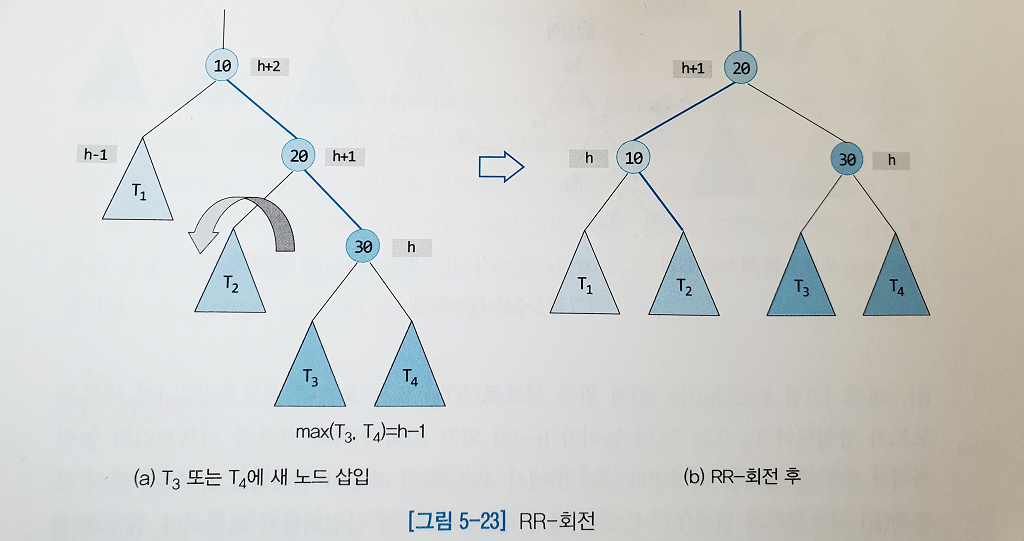
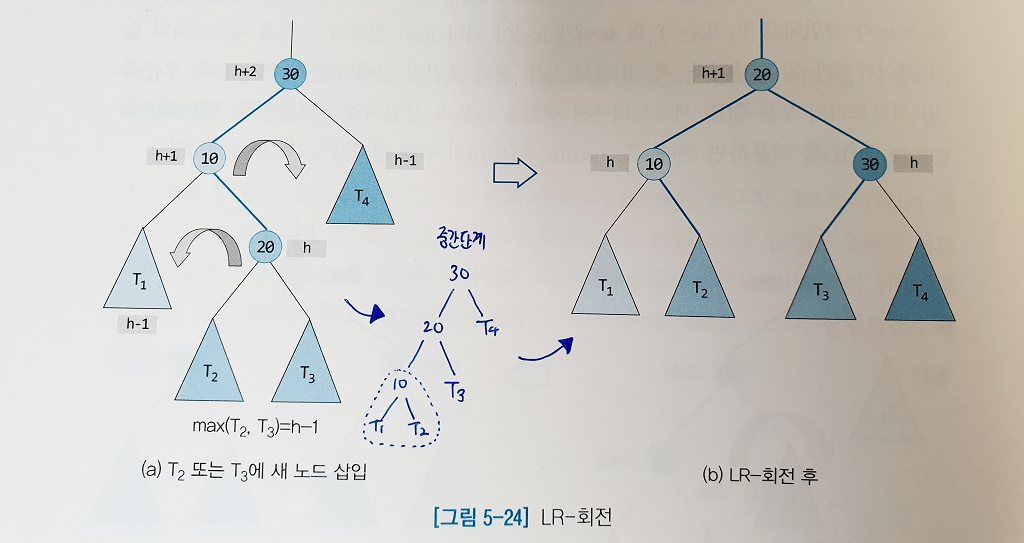
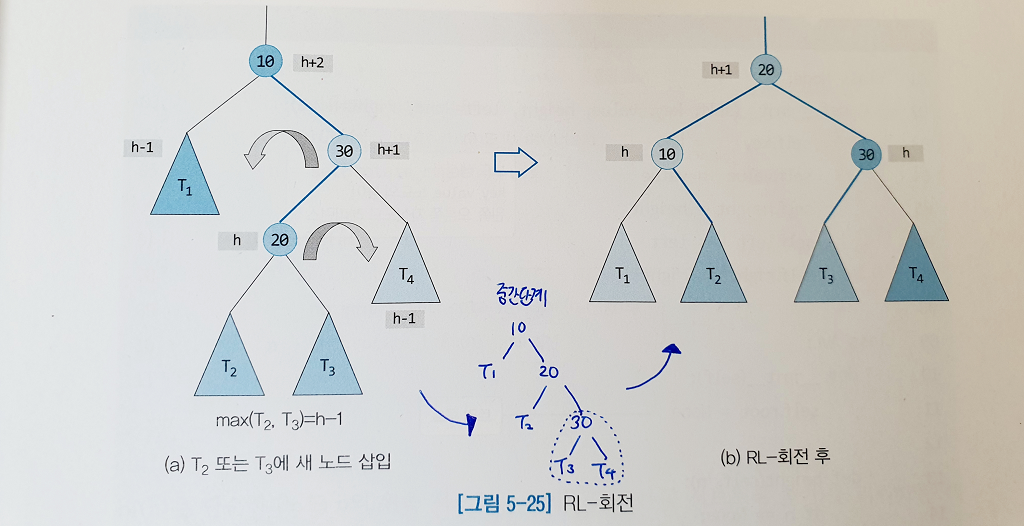
# 우회전
def rotate_right(self, node):
temp = node.left
node.left = temp.right
temp.right = node
node.height = max(self.height(node.left), self.height(node.right)) + 1
temp.height = max(self.height(node.left), self.height(temp.right)) + 1
return temp
# 좌회전
def rotate_left(self, node):
temp = node.right
node.right = temp.left
temp.left = node
node.height = max(self.height(node.left), self.height(node.right)) + 1
temp.height = max(self.height(temp.left), self.height(temp.right)) + 1
return temp
# 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이 반환하기
def bf(self, node):
return self.height(node.left) - self.height(node.right)
# 불균형 없애기
def balance(self, node):
if self.bf(node) > 1:
if self.bf(node.left) < 0: # 왼쪽 자식의 오른쪽 서브트리가 높은 경우 LR 회전하기
node.left = self.rotate_left(node.left)
node = self.rotate_right(node) # 왼쪽 자식의 왼쪽 서브트리가 높은 경우에는 LL 회전하기
elif self.bf(node) < -1:
if self.bf(node.right) > 0: # 오른쪽 자식의 왼쪽 서브트리가 높은 경우에는 RL 회전하기
node.right = self.rotate_right(node.right)
node = self.rotate_left(node) # 오른쪽 자식의 오른쪽 서브트리가 높은 경우에는 RR 회전하기
return node
임의의 키값을 가지는 노드 삽입하기
# key와 value를 키값과 항목으로 가지는 노드 삽입하기
def put(self, key, value):
self.root = self.put_item(self.root, key, value)
def put_item(self, node, key, value):
if node == None:
return Node(key, value, 1)
if node.key > key:
node.left = self.put_item(node.left, key, value)
elif node.key < key:
node.right = self.put_item(node.right, key, value)
else:
node.value = value
return node
node.height = max(self.height(node.left), self.height(node.right)) + 1 # 노드의 높이 갱신하기
return self.balance(node) # 노드의 균형 유지하기
임의의 키값을 가지는 노드 삭제하기
# 키값이 key인 노드 삭제하기
def delete(self, key):
self.root = self.del_node(self.root, key)
def del_node(self, node, key):
if node == None:
return None
if node.key > key:
node.left = self.del_node(node.left, key)
elif node.key < key:
node.right = self.del_node(node.right, key)
else:
if node.right == None:
return node.left
if node.left == None:
return node.right
target = node
node = self.minimum(target.right)
node.right = self.del_min(target.right)
node.left = target.left
node.height = max(self.height(node.left), self.height(node.right)) + 1 # 노드의 높이 갱신하기
return self.balance(node) # 노드의 균형 유지하기
2-3 트리
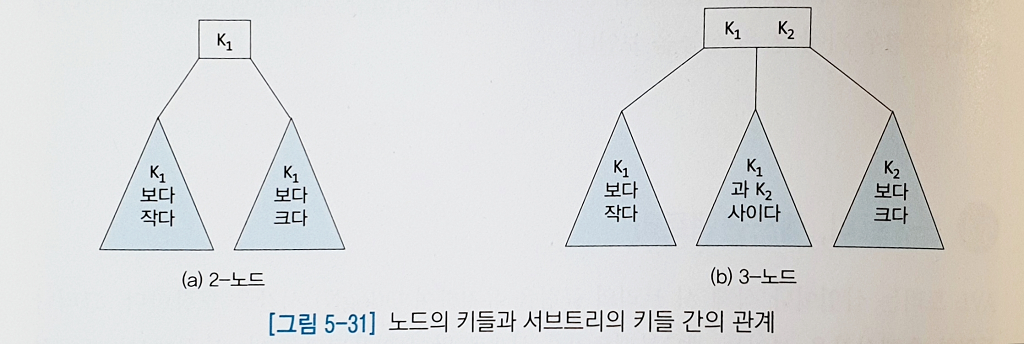
2-3 트리는 이파리의 레벨이 전부 동일하며 차수가 2이거나 3인 노드로만 구성된 트리이다. 차수가 2인 노드를 2-노드라 하고 차수가 3인 노드를 3-노드라 한다. 노드의 키값과 서브트리의 키값들 사이의 관계는 이진탐색트리에서와 같다.
좌편향 레드블랙트리(left-leaning red-black tree)
좌편향 레드블랙트리는 아래의 조건을 만족하는 이진탐색트리이다. 2-3 트리에서 3-노드에 있는 2개의 키를 2개의 노드로 분리하여 저장한 뒤 왼쪽을 레드 오른쪽을 블랙으로 칠한 형태와 동일하다 볼 수 있다. AVL 트리, 2-3 트리보다 성능이 우수하다고 알려져 있다.
- 루트와
None은 블랙임 - 루트로부터 각각의
None까지 2개의 연속된 레드link가 존재할 수 없음 - 루트로부터 각각의
None까지의 경로에 있는 블랙link의 수는 전부 같음 - 레드
link는 왼쪽으로 기울어져 있음
B-트리
B-트리는 노드에 수백에서 수천 개의 키를 저장하여 높이를 낮춘 트리이다. 아래의 조건을 만족하는 트리를 차수가 M인 B-트리라 한다. 키의 삽입에는 분리 연산이, 키의 삭제에는 이동 연산과 통합 연산을 사용한다 알려져 있다. 탐색, 삽입, 삭제 연산을 수행하는 데 걸리는 시간은 B-트리의 높이에 비례한다. 차수가 \(M\)이고 키의 개수가 \(N\)인 B-트리의 최대 높이는 \(O(log_{M/2}N)\)이다.
- 이파리의 레벨은 전부 동일함
- 각 내부노드의 자식 수는 \(\left \lceil{M/2}\right \rceil\) 이상 \(M\) 이하임
- 루트의 차수는 2 이상임
Reference 파이썬과 함께하는 자료구조의 이해 / 양성봉 지음 / 생능출판사
