정점(vertex)들과 두 개의 정점을 잇는 간선(edge)들의 집합인 그래프(graph)는 광범위한 분야에 활용되는 자료구조이다. 그래프에 관한 용어들을 정리한 다음, 그래프에 속한 정점들을 빠짐없이 방문하는 두 가지 기본 연산인 깊이 우선 탐색(depth first search)과 너비 우선 탐색(breadth first search)을 구현했다. 그리고 최소 신장 트리(minimum spanning tree)를 찾는 Kruskal 알고리즘과 Prim 알고리즘, 최단 경로(shortest path)를 찾는 Dijkstra 알고리즘과 Floyd-Warshall 알고리즘에 대해 정리했다.

그래프(graph)
깊이 우선 탐색(depth first search)
너비 우선 탐색(breadth first search)
최소 신장 트리(minimum spanning tree)
- Kruskal
- Prim
최단 경로(shortest path)
- Dijkstra
- Floyd-Warshall

그래프(graph)

그래프에 대한 용어에는 아래와 같은 것들이 있다.

용어	정의
방향 그래프(directed graph)	간선에 방향이 있는 그래프
무방향 그래프(undirected graph)	간선에 방향이 없는 그래프
가중치 그래프(weighted graph)	간선에 가중치가 부여된 그래프
차수(degree)	(무방향 그래프에서) 주어진 정점에 인접한 정점의 수
진입 차수(in-degree)	(방향 그래프에서) 주어진 정점으로 들어오는 간선의 수
진출 차수(out-degree)	(방향 그래프에서) 주어진 정점에서 나가는 간선의 수
경로(path)	인접한 정점들의 나열
단순 경로(simple path)	정점들이 겹치지 않는 경로
사이클(cycle)	시작 정점과 끝 정점이 일치하는 단순 경로
부분 그래프(subgraph)	주어진 그래프의 일부 정점과 일부 간선으로 이루어진 그래프
희소 그래프(sparse graph)	정점의 차수가 작은 그래프
조밀 그래프(dense graph)	정점의 차수가 커서 간선의 수가 최대 간선 수에 가까운 그래프
연결성분(connected component)	임의의 두 정점 사이에 경로가 존재하는 최대 크기의 부분 그래프
단절 정점(articulation point)	연결성분에서 하나의 단절 정점을 삭제하면 두 개 이상의 연결성분으로 분리됨
이중연결성분(biconnected component)	(무방향 그래프에서) 단절 정점이 존재하지 않는 연결성분
강연결성분(strongly connected component)	(방향 그래프에서) 임의의 두 정점 `v1`과 `v2`에 대해 `v1`에서 `v2`으로 가는 경로와 `v2`에서 `v1`으로 가는 경로가 존재하는 연결성분
신장 트리(spanning tree)	하나의 연결성분으로 구성된 그래프에서 모든 정점들을 사이클 없이 연결하는 부분그래프

그래프를 저장하기 위해 일반적으로 인접행렬(adjacency matrix)과 인접리스트(adjacency list)를 사용한다(둘 다 중첩 리스트임).

용어	정의
인접행렬	(무방향 그래프에서) 정점 `i`와 `j`를 잇거나 (방향 그래프에서) 정점 `i`에서 `j`로 향하는 간선이 존재하면 `A[i][j]`의 값은 1이고 아니면 0임
인접리스트	`A[i]`의 값은 정점 `i`에 인접한 다른 정점들의 리스트임

깊이 우선 탐색(depth first search)

(1)

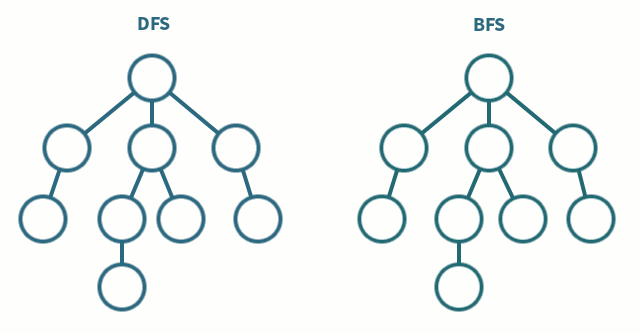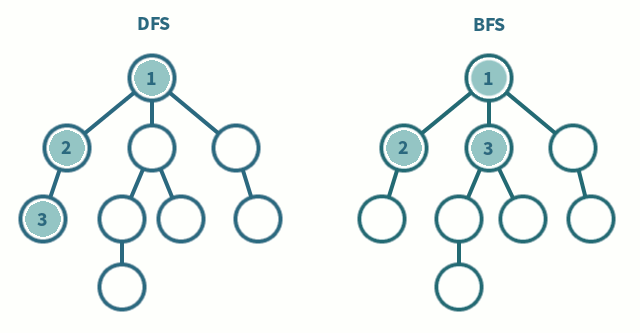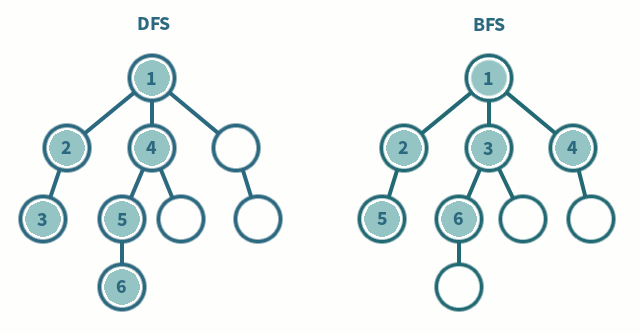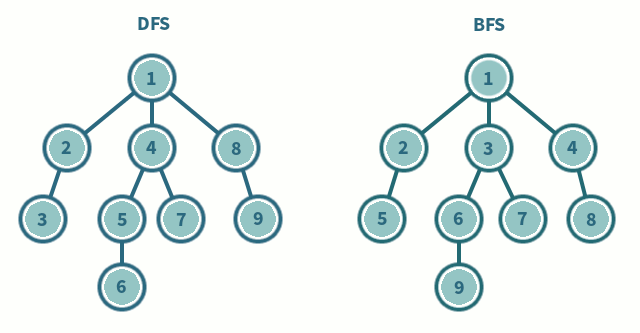
그래프가 인접리스트로 저장되어 있는 경우 깊이 우선 탐색(depth first search)과 너비 우선 탐색(breadth first search)을 사용하면 \(O(V+E)\)의 시간에 정점들을 빠짐없이 방문할 수 있다(\(V\)는 정점의 수이고 \(E\)는 간선의 수임). 임의의 정점에서부터 깊이 우선 탐색을 하는 경우 인접한 정점을 방문한 뒤 방금 방문한 정점에 인접한 다른 정점을 방문하는 식으로 탐색이 일어난다. 더 이상 인접한 정점에 방문할 수 없다면 아직 방문하지 않은 다른 정점에서부터 탐색을 다시 시작한다.

 def DFS(adj_list):  # adj_list는 인접리스트임
        
    visited = [False] * len(adj_list)  # visited[i]의 값은 정점 i를 방문했다면 True이고 아니면 False임
    dfs_list = []  # 방문한 정점들이 담길 리스트임
       
    def dfs(v):  # 정점 v에서부터 탐색 시작하기
    
        visited[v] = True  # 정점 v를 방문하기
        dfs_list.append(v)  # 정점 v를 dfs_list에 담기
        
        for adj_v in adj_list[v]:  # 방금 방문한 정점 v에 인접한 정점들 adj_v에 대해서
            if not visited[adj_v]:  # adj_v를 아직 방문하지 않았다면
                dfs(adj_v)  # adj_v에서부터 다시 탐색 시작하기
        
    for v in range(len(adj_list)):
        if not visited[v]:
            dfs(v)
            
    return dfs_list

특별히 그래프가 트리 형태인 경우, DFS를 통해 리프 노드에서 루트 노드로 거슬러 올라갈 수 있다. 리프 노드에서 함수 호출이 종료되기 때문이다. visited 배열을 만들 필요도 없다.

def dfs(parent, node):
    for child in adj_list[node]:  # adj_list는 인접딕셔너리
        if child != parent:
            dfs(node, child)
    print('node: %d -> parent: %d' %(node, parent))
        
dfs(None, root)  # root의 parent는 없음

adj_list = {
[2, 4, 8],
[1, 3],
[2],
[1, 5, 7],
[4, 6],
[5],
[4],
[1, 9], 
[8]
}

child: 2 -> parent: 3
child: 1 -> parent: 2
child: 5 -> parent: 6
child: 4 -> parent: 5
child: 4 -> parent: 7
child: 1 -> parent: 4
child: 8 -> parent: 9
child: 1 -> parent: 8
child: 1 -> parent: 1

연결성분(connected component) 찾기

깊이 우선 탐색을 변형하여 무방향그래프에서 연결성분을 찾을 수 있다.

def CC(adj_list):  # adj_list는 인접리스트임

    visited = [False] * len(adj_list)  # visited[i]의 값은 정점 i를 방문했다면 True이고 아니면 False임
    CClist = []  # 연결성분들이 담길 리스트임
        
    def dfs(v):  # 정점 v에서부터 탐색 시작하기
    
        visited[v] = True  # 정점 v를 방문하기
        cclist.append(v)  # 정점 v를 연결성분에 담기
        
        for adj_v in adj_list[v]:  # 방금 방문한 정점 v에 인접한 정점들 adj_v에 대해서
            if not visited[adj_v]:  # adj_v를 아직 방문하지 않았다면
                dfs(adj_v)  # adj_v에서부터 다시 탐색 시작하기
                
        # 정점 v와 연결된 정점들을 전부 방문했다면 함수는 더 이상 실행되지 않음
        
    for v in range(len(adj_list)):
        if not visited[v]:  # 정점 v를 아직 방문하지 않았다면
            cclist = []  # 정점 v가 속해 있는 연결성분을 담을 리스트 초기화하기
            dfs(v)  # 정점 v와 연결된 정점들을 전부 방문하여 연결성분에 담기
            CClist.append(cclist)  # CClist에 정점 v가 속해 있는 연결성분을 담기
        
    return CClist

강연결성분(strongly connected component) 찾기

Kosaraju 알고리즘은 깊이 우선 탐색을 활용하여 방향 그래프에서 강연결성분을 찾는다. 주어진 방향 그래프와 역방향 그래프의 강연결성분은 완전히 동일하다는 사실을 이용하지만 증명은 어려워서 이해하지 못했다.

def Kosaraju(adj_matrix):  # adj_list는 인접행렬임
    
    N, stack, BCClist = len(adj_matrix), [], []
    
    def dfs(v):
        visited[v] = True
        for adj_v in range(N):
            if adj_matrix[v][adj_v] == 1 and not visited[adj_v]:
                dfs(adj_v)
        stack.append(v)
        
    def rev_dfs(v):
        visited[v] = True
        for adj_v in range(N):
            if adj_matrix[adj_v][v] == 1 and not visited[adj_v]:
                rev_dfs(adj_v)
        bcclist.append(v)  
        
    visited = [False] * N
    for v in range(N):
        if not visited[v]:
            dfs(v)
    
    visited = [False] * N
    while stack:
        v = stack.pop()
        if not visited[v]:
            bcclist = []
            rev_dfs(v)
            BCClist.append(bcclist)
    
    return BCClist

위상 정렬(topological sort) 하기

위상 정렬(topological sort)은 사이클이 없는 방향 그래프(directed acyclic graph)에서 각 정점들을 간선의 방향에 맞추어 나열한다. 깊이 우선 탐색에서와 달리 정점 v에서 출발하여 도착할 수 있는 정점들을 전부 방문한 후에 정점 v를 리스트에 담는다. 이때 정점 v 이전에 리스트에 담긴 정점들은 전부 정점 v에서 출발하여 도착할 수 있는 정점들이 되기에 리스트를 역순으로 출력하면 위상 정렬을 할 수 있다.

def TS(adj_list):  # adj_list는 인접리스트임

    visited = [False] * len(adj_list)  # visited[i]의 값은 정점 i를 방문했다면 True이고 아니면 False임
    TSlist = []  # 방문한 정점들이 담길 리스트임
    
    def dfs(v):  # 정점 v에서부터 탐색 시작하기
    
        visited[v] = True  # 정점 v를 방문하기
        
        for adj_v in adj_list[v]:  # 정점 v에서 출발하여 도착할 수 있는 정점들 adj_v에 대해
            if not visited[adj_v]:  # adj_v를 아직 방문하지 않았다면 
                dfs(adj_v)  # adj_v에서부터 다시 탐색 시작하기
                
        TSlist.append(v)  # 정점 v에서 출발하여 도착할 수 있는 정점들을 전부 방문했다면 리스트에 정점 v 담기
        
    for v in range(len(adj_list)):
        if not visited[v]:
            dfs(v)
    
    return list(reversed(TSlist))

너비 우선 탐색(breadth first search)

임의의 정점에서부터 너비 우선 탐색을 하는 경우 인접한 정점을 전부 방문한 다음에 그 인접한 정점들에 인접한 다른 정점을 전부 방문하는 식으로 탐색이 일어난다(트리에서의 레벨순회와 동일함).

def BFS(adj_list):  # adj_list는 인접리스트임
    
    visited = [False] * len(adj_list)  # visited[i]의 값은 정점 i를 방문했다면 True이고 아니면 False임
    bfs_list = []  # 방문한 정점들이 담길 리스트임
    
    def bfs(v):  # 정점 v에서부터 탐색 시작하기
    
        visited[v] = True  # 정점 v를 방문하기
        queue = [v]  # 방문한 정점들을 담아둘 큐 만들기
        
        while len(queue) > 0:  # 큐가 빌 때 까지
        
            v = queue.pop(0)  # 큐에서 맨 앞에 있던 정점 v를 꺼내기
            bfs_list.append(v)  # 이미 방문한 정점 v를 bfs_list에 담아주기
            
            for adj_v in adj_list[v]:  # 정점 v에 인접한 정점들 adj_v에 대해
                if not visited[adj_v]:  # adj_v를 아직 방문하지 않았다면
                    visited[adj_v] = True  # adj_v를 방문한 다음
                    queue.append(adj_v)  # 큐에 담기
    
    for v in range(len(adj_list)):
        if not visited[v]:
            bfs(v)
    
    return bfs_list

최소 신장 트리(minimum spanning tree)

하나의 연결성분으로 이루어진 무방향 가중치 그래프에 대해 간선들의 가중치 합이 가장 작은 신장 트리를 최소 신장 트리(minimum spanning tree)라 한다. 최소 신장 트리를 찾기 위한 Kruskal 알고리즘과 Prim 알고리즘은 탐욕(greedy) 알고리즘의 일종으로 욕심내 선택한 지역적인 최적해를 누적해 전체적인 최적해를 얻는다. 수행 시간은 둘 다 \(O(ElogV)\)이다(\(V\)는 정점의 수이고 \(E\)는 간선의 수임).

`Kruskal`

주어진 그래프에 \(N\)개의 정점이 존재할 때 가중치가 가장 작은 간선이 사이클을 형성하지 않는다면 트리에 포함시키는 수행을 \(N - 1\)번 반복하면 최소 신장 트리를 얻을 수 있다.

(2)

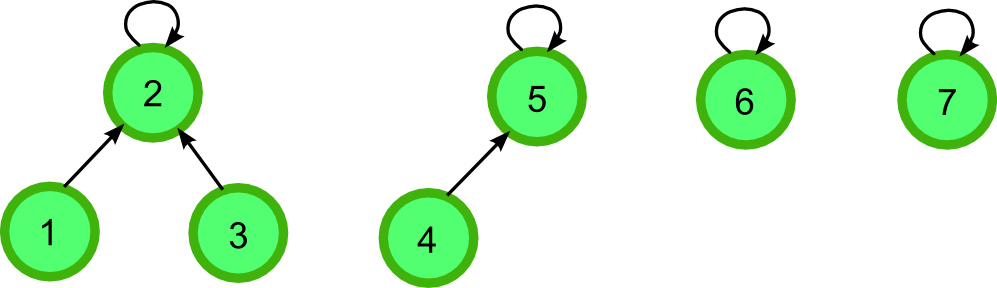
사이클이 생기는지를 검사하기 위해서는 서로소 집합(disjoint set) 자료구조를 사용한다. 임의의 두 집합을 선택했을 때 교집합이 공집합이 되는 집합들이 서로소 집합 자료구조를 구성하는데, 이때 존재하는 모든 집합들의 모든 원소가 \(0, 1, 2, \cdots, N - 1\)이라면 길이가 \(N\)인 리스트 parent에 서로소 집합을 저장할 수 있다. 하나의 집합을 하나의 트리로 나타낸 뒤에 parent[i]의 값을 i의 부모로 하면 되기 때문이다(i가 루트일 경우 parent[i]의 값은 i임). 예를 들어 위와 같은 서로소 집합 자료구조의 경우 {2, 1, 3}, {5, 4}, {6}, {7}이라는 집합으로 구성되며 parent는 [None, 2, 2, 2, 5, 5, 6, 7]가 됨을 알 수 있다.

def Kruskal(graph, N):  # graph는 (정점1, 정점2, 가중치)의 리스트
                        # N은 정점의 개수임

    def find(v):  # v의 루트 찾기
        if v != parent[v]:  # v가 루트가 아니라면
            parent[v] = find(parent[v])  # v의 부모에서 다시 find 수행하면서 경로 압축하기
        return parent[v]  # v의 부모 반환하기
    
    def union(v1, v2):  # v1과 v2가 속한 집합을 합치기
        root1, root2 = find(v1), find(v2)  # v1과 v2의 루트 찾기
        parent[root2] = root1  # v2가 속한 집합의 루트의 부모를 v1의 루트로 갱신하기

서로소 집합에서 수행할 수 있는 연산에는 find와 union이 있다. find(v)는 v가 속한 집합의 루트를 반환한다. 이때 루트까지 올라가며 만나는 노드의 부모를 루트로 갱신하는 과정인 경로 압축(path compression)이 일어난다. 이는 추후 실행되는 find 연산의 수행 시간을 단축시킨다. union(v1, v2)는 v1과 v2가 속한 집합을 합치기 위해 v2가 속한 집합의 루트의 부모를 v1이 속한 집합의 루트로 갱신해준다.

    graph.sort(key = lambda x: x[2])  # graph를 가중치 순으로 정렬하기
    
    parent = []  # 서로소 집합을 나타낼 리스트임
    for i in range(N):  # 아직 트리에 포함된 정점이 없으므로
        parent.append(i)  # 각각의 정점의 루트는 자기 자신임
        
    mst = []  # 트리에 포함시킬 간선들이 담길 리스트임
    cost = 0  # 트리에 포함된 간선들의 가중치 합임
    
    while True:
    
        if len(mst) == N - 1:  # 트리에 존재하는 간선이 N - 1개가 되면
            break  # 실행 중지하기
            
        v1, v2, weight = graph.pop(0)  # 가중치가 가장 작은 간선 뽑기
        
        if find(v1) != find(v2):  # v1과 v2가 다른 집합에 존재하면 사이클이 생기지 않으므로
            mst.append([v1, v2])  # 뽑은 간선을 트리에 추가하기
            union(v1, v2)  # v1과 v2가 트리에 추가되었으므로 v1과 v2가 속한 집합을 합치기
            cost += weight  # weight에 뽑은 간선의 가중치 더하기
    
    return mst, cost

# cost만 구하는 clean version
def Kruskal(graph, N):

    def find(v):
        if v != parent[v]:
            parent[v] = find(parent[v])
        return parent[v]

    def union(v1, v2):
        root1, root2 = find(v1), find(v2)
        parent[root2] = root1

    graph.sort(key = lambda x: x[2])

    parent = []
    for i in range(N):
        parent.append(i)

    cost = 0; edge = 0;
    while True:
        if edge == N - 1:
            break
        v1, v2, weight = graph.pop(0)
        if find(v1) != find(v2):
            union(v1, v2)
            cost += weight
            edge += 1

    return cost

`Prim`

주어진 그래프에 \(N\)개의 정점이 존재할 때 임의의 정점 start만을 가지는 트리에서 시작하여 트리에 속한 정점의 수가 \(N\)이 될 때 까지 트리에 인접한 정점들 중에서 가중치가 가장 작은 간선으로 연결된 것을 트리에 추가하는 작업을 반복하여 최소 신장 트리를 얻는다.

import sys

def Prim(graph, start, N): # graph[v]는 정점 v에 인접한 (정점, 가중치)의 리스트
                           # start는 트리에 처음으로 추가될 정점임
                           # N은 정점의 개수임
    
    visited = [False] * N  # visited[i]의 값은 정점 i가 트리에 속하면 True이고 아니면 False임    
    D = [sys.maxsize] * N 
    previous = [None] * N  # previous[i]의 값은 D[i]의 값을 갱신시킨 정점임 
    
    D[start], previous[start] = 0, start
    
    vertices = 1  # 트리에 추가된 정점의 수
    while True:
     
        if vertices == N:  # 트리에 존재하는 정점의 수가 N이 되면
            break  # 실행 중지하기
        
        min_vertex = -1  # min_vertex는 트리에 인접한 정점들 중 가중치가 가장 작은 간선으로 연결된 것임
        min_value = sys.maxsize  # min_value는 이 간선의 가중치임
        
        for v in range(N):
            if not visited[v] and D[v] < min_value:
                min_vertex = v
                min_value = D[v]
                
        visited[min_vertex] = True  # min_vertex를 트리에 추가하기
        vertices += 1
        
        for adj_v, weight in graph[min_vertex]:  # min_vertex에 인접한 정점들인 adj_v에 대해
            if not visited[adj_v]:  # adj_v가 트리에 속하지 않은 동시에
                if weight < D[adj_v]:  # min_vertex와 adj_v를 잇는 간선의 가중치가 D[adj_v]보다 작다면
                    D[adj_v] = weight  # D[adj_v] 갱신하기
                    previous[adj_v] = min_vertex  # D[adj_v]가 min_vertex에 의해 갱신되었음을 나타내기
    
    mst = [[v, previous[v]] for v in range(1, N)]  # mst는 트리에 추가된 간선들의 집합
    cost = sum(D[1:])  # cost는 트리에 추가된 간선들의 가중치 합
    
    return mst, cost

최단 경로(shortest path)

주어진 가중치 그래프에서 출발 정점과 도착 정점을 연결하는 경로 중 간선의 가중치 합이 가장 작은 것을 찾는 방법에는 Dijkstra 알고리즘과 Floyd-Warshall 알고리즘이 있다.

`Dijkstra`

Dijkstra 알고리즘을 사용하면 주어진 출발 정점에서부터 나머지 정점들까지의 최단 경로를 구할 수 있다. Prim 알고리즘과 매우 유사하지만 Dijkstra 알고리즘의 경우 D[i]에 출발 정점에서 정점 i까지의 최단 경로의 길이(간선의 가중치의 합)가 저장된다는 점에서 차이가 있다. 수행시간은 \(O(V^{2})\)이다(\(V\)는 정점의 수임). 음수 가중치가 있는 경우에는 실패할 수 있다는 것이 단점이다.

import sys

def Dijkstra(graph, start, N): # graph[v]는 정점 v에 인접한 (정점, 가중치)의 리스트임
                               # start는 출발 정점임
                               # N은 정점의 개수임
    
    visited = [False] * N  # visited[i]의 값은 정점 i가 트리에 속하면 True이고 아니면 False임
    D = [sys.maxsize] * N  # D[i]의 값은 출발 정점에서 정점 i까지의 최단 거리임
    previous = [None] * N  # previous[i]의 값은 D[i]의 값을 갱신시킨 정점임
    
    D[start], previous[start] = 0, start
    
    vertices = 1
    while True:
        
        if vertices == N:  # 트리에 존재하는 정점의 수가 N이 되면
            break  # 실행 중지하기
        
        min_vertex = -1  # min_vertex는 트리에 인접한 정점들 중 가중치가 가장 작은 간선으로 연결된 것임
        min_value = sys.maxsize  # min_value는 이 간선의 가중치임
        for v in range(N):
            if not visited[v] and D[v] < min_value:
                min_vertex = v
                min_value = D[v]
        visited[min_vertex] = True
        vertices += 1
        
        for adj_v, weight in graph[min_vertex]:  # min_vertex에 인접한 정점들인 adj_v에 대해
            if not visited[adj_v]:  # adj_v가 트리에 속하지 않은 동시에
                if D[min_vertex] + weight < D[adj_v]:  # 출발 정점부터 min_vertex를 경유하여 adj_v로 가는 최단 거리가 기존 최단거리인 D[adj_v]보다 짧다면
                    D[adj_v] = D[min_vertex] + weight  # D[adj_v] 갱신하기
                    previous[adj_v] = min_vertex  # D[adj_v]가 min_vertex에 의해 갱신되었음을 나타내기

    path = []
    
    path = []
    for v in range(N):
        
        v_path = []
        
        if D[v] == sys.maxsize:
            v_path = [None]
        
        else:        
            prev_v = v
            while prev_v != start:
                v_path.append(prev_v)
                prev_v = previous[prev_v]
            v_path.append(start)
            v_path.reverse()

        path.append(v_path)
    
    return list(zip(path, D))

`Floyd-Warshall`

Floyd-Warshall 알고리즘을 사용하면 모든 정점 쌍 사이의 최단경로를 얻을 수 있다. 수행 시간은 \(O(V^{3})\)이다(\(V\)는 정점의 수임). Dijkstra 알고리즘과 달리 음수 가중치가 있어도 성공한다.

import sys

def floyd_warshall(adj_matrix):  # adj_matrix는 인접행렬임
                                 # (adj[i][j]의 값은 정점 i와 j가 인접하면 간선의 가중치이고 아니면 sys.maxsize)
    
    N = len(adj_matrix)
    
    for count in range(N):
        for i in range(N):
            for j in range(N):
                adj_matrix[i][j] = min(adj_matrix[i][j], adj_matrix[i][count] + adj_matrix[count][j])

    return adj_matrix

Reference 파이썬과 함께하는 자료구조의 이해 / 양성봉 지음 / 생능출판사

파이썬 자료구조: 그래프

Categories

Tags